¿COMO LE HICIERON LOS GRIEGOS PARA CALCULAR EL PERÍMETRO DE UNA CIRCUNFERENCIA?
¿Cómo Eratóstenes midió la circunferencia de la tierra hace 2 mil años?
El matemático griego Eratóstenes, se dio cuenta de que en el día del solsticio de verano (21 de junio) al medio día, en la ciudad de Siena (hoy Asuán) la luz del sol no proyectaba ninguna sombra sobre el fondo de un pozo, pero en la ciudad de Alejandría, situada al norte de Siena, en el mismo día y a la misma hora sí se proyectaba una sombra sobre el fondo de un pozo.
El solsticio de verano es el día mas largo del año y es producido por la inclinación del eje de la tierra. En el solsticio de verano del hemisferio Norte el Sol alcanza el cenit al mediodía sobre el Trópico de Cáncer, es decir, que en los lugares situados allí, el 21 de junio los rayos del sol caen verticalmente sobre la tierra, y por supuesto como esta es redonda, en los demás lugares caen inclinadamente. La ciudad de Siena esta ubicada muy cerca de la línea del trópico de cáncer.
La observación de Eratóstenes confirmaba algo que otros griegos ya sospechaban: que la tierra era redonda; puesto que si fuera plana, en Alejandría no debería proyectarse ninguna sombra sobre el pozo al igual que en Siena. Además, porque se nota la curvatura en el cielo, porque mientras mas uno viaja al norte hay estrellas y constelaciones que se ven cada vez mas arriba como la de Polaris, y otras que simplemente desaparecen en horizonte como la de Canopus.
Hechas estas observaciones a Eratóstenes se le ocurrió una brillante idea. El día 21 de junio al medio día en Alejandría tomó un palo y midió el ángulo de la sombra que se proyectaba sobre este y anotó que era una cincuentava parte de un circulo (en aquellos tiempos no existían las nociones de grados). La 50ava parte de un circulo (360 grados) equivale a 7.2 grados.
Entonces como ese mismo día a esa misma hora los rayos del sol caían verticalmente sobre Siena proyectando sombras de 0 grados sobre una vertical, entonces entre Siena y Alejandría había una distancia de 7.2 grados o la 50ava parte de la circunferencia de la tierra. (Eratóstenes asumió que la tierra era perfectamente circular).
Eratóstenes ya sabia de las caravanas que comerciaban entre ambas ciudades, que había una distancia estimada de 5,000 estadios entre ellas. Por lo tanto, simplemente multiplicó por 50. Esto es 250,000 estadios. El estadio era la unidad griega de longitud, que variaba de una localidad a otra entre 157.5 metros a 184.8 metros. El estadio utlizado por Eratóstenes fue el ático-italiano de 184.8 metros. Esto es 46,200 kms.
En las primera gráfica la maqueta esta inclinada pero en dirección al sol, no se produce sombra. En la segunda se inclino la maqueta pero manteniendola recta y la sombra que se produce en ambas es igual. En la tercera y cuarta gráfica entonces se curva la maqueta dejando el primer palito en dirección al sol, y vemos como en el segundo palito la sombra es larga pero en el primero no hay.


Debemos aclarar algo antes de continuar: ¿Cómo Eratóstenes midió el ángulo de la sombra que se proyectaba? Lamentablemente el libro escrito por el propio Eratóstenes: “Sobre las medidas de la tierra”, que nos brindaría detalles sobre sus descubrimientos; se perdió, al igual que pasó también con muchos otros escritos de la antiguedad; que no sobrevivieron a las destrucciones de la biblioteca de Alejandria (por maremoto, incendios de invasores) y de la cual Eratóstenes fue su tercer director. El astrónomo griego Cleómedes en su obra “sobre el movimiento de los cuerpos celestes” que es la principal fuente original a través de la cual conocemos de los descubrimiento de Eratóstenes, solo dice que este utilizó un gnómon, que es un palo o estilete vertical que proyecta su sombra sobre una superficie horizontal, pero no dice cómo midió la sombra que se proyectaba, pero a partir de esto solo hay dos maneras posibles de hacerlo: La primera y la que todos conocemos, es utilizando funciones trigonométricas. En este caso sería hallando el valor de la tangente, es decir, la medida de la sombra dividido entre la medida de la vara (cateto opuesto sobre cateto adyacente), y luego le sacamos la arcotangente ( tan-1) con la calculadora para obtener el ángulo de la tangente, y opcionalmente la llevamos a grados con el botón (.,,,) de la Casio. Pero las complejidades y abstractismo del cálculo diferencial e integral no estaban disponibles para aquella época.
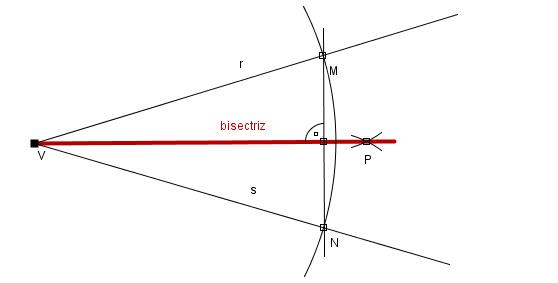
En mi afán por resolver este misterio, descubrí o redescubrí una técnica sencilla pero olvidada, utilizando simplemente un compás. Simplemente Eratóstenes trazaría a escala en un plano (o en un papiro) la medida de la vara y de la sombra en el suelo y le trazaría la hipotenusa, luego voltearía el plano para comodidad por supuesto, quedando el lado opuesto a la hipotenusa (o la medida a escala del gnomon) como una recta horizontal e interpondría un compás con un lado en el vértice que se forma entre la hipotenusa y la medida del gnomon y trazaría un circulo alrededor. Luego en el punto en el que la hipotenusa intersecta con la circunferencia se coloca un lado del compás y el otro lado del compás se coloca más abajo en el punto en donde la circunferencia trazada toca con la recta horizontal. Dejamos el compás con esa misma medida y empezamos a medir sobre la circunferencia cuantas partes de ella equivalen. Pero Eratóstenes tampoco tuvo que haber utilizado un compás necesariamente; cualquier vertical que gire sobre su propio eje, formará un círculo perfecto.
Utilicé el programa “regla y compás” para construir digital y exactamente la circunferencia y los ángulos. Como podemos ver la mitad de la circunferencia que elaboré está dividida en 25 partes iguales de 7.2 grados.
Pueden interponer un transportador transparente o un compás sobre la pantalla y comprobarlo ustedes mismos.
Abajo tenemos compases de la época greco-romana guardados en el museo británico.
Ahora tenemos un simple gnomon que utilizaría Eratóstenes y luego tres gnomons utilizados para marcar la hora (relojes solares).
La medida de la circunferencia de la tierra, realizada por satélites avanzados, es de 40,008 kms aproximadamente. Si tomamos en cuenta la simpleza y rudimentaria, aunque ingeniosa técnica utilizada por Eratóstenes, la aproximación de su cálculo fue asombrosa. Solo se equivocó en 6,192 kms. Esto es un 15%.
Ahora bien, utilicemos las poderosas herramientas tecnológicas que poseemos hoy día, MapCrow y Google Map, y rehagamos el cálculo de Eratóstenes con medidas exactas a ver si su razonamiento era correcto.
La latitud es la distancia angular aproximada entre la línea ecuatorial y un punto determinado del planeta. Son las líneas horizontales que hay en un mapa. Se expresan en medidas angulares que varían desde los cero grados del ecuador hasta los 90 grados del polo Norte o los 90° del polo Sur. Si trazamos una recta que vaya desde un punto cualquiera de la tierra hasta el centro de la misma, el ángulo que forma esa recta con el plano ecuatorial expresa la latitud de dicho punto.
Antes de continuar, hay 3 supuestos que debemos tomar en cuenta:
1) Suponemos que la tierra es perfectamente redonda. Un grado de latitud no mide exactamente lo mismo en cada lugar, sino que varía ligeramente de 110,57 km en el ecuador hasta 111,70 km en los polos, por eso no podemos asumir que 7 grados entre Alejandria y Siena tendrán la misma distancia que 7 grados entre Alejandria y alguna ciudad de Turquía. Por eso nuestro resultado no podría ser nunca exactamente igual al que hicieron los avanzados satélites de millones de dólares.
2) Si hacemos la resta de las longitudes (las líneas verticales del mapa) hay una diferencia de 3 grados (Eratóstenes suponía que estaban en la misma longitud).
3) Otro pequeño error de Eratóstenes, es que realmente Siena no estaba ubicada exactamente sobre la línea del trópico de cáncer (los puntos donde los rayos del sol caen a la tierra verticalmente el 21 de junio). Hoy día esta a 72 kms (desde el centro de la ciudad). Pero debido a que las variaciones del eje de la tierra fluctúan de entre 22.1 y 24.5 grados en un período de 41 mil años, hace 2 mil años estaba ubicada a 41 kms -Para calcular las coordenadas de la línea del trópico utilicé la aplicación de neoprogrammics.com y calculé los valores para el año -200.-
Veamos:
Si hacemos la resta de las latitudes, habría una distancia angular de 7.1106 o 7º 6′ entre ambas ciudades. Esto significa que la distancia entre Alejandría y Asuán sería una 50.6286ava parte de una circunferencia (360 grados). A Eratóstenes le dio una 50ava parte de una circunferencia que es 7.1997 o 7º 12′.
La distancia no es de 924 kms, sino de 843 kms. 81 kms de diferencia -Distancia aérea y hasta el centro de las ciudades.-
El cálculo corregido de Eratóstenes da como resultado 42, 662 kms. El error es de solo 2,654 kms o 6.6 %.
El razonamiento de Eratóstenes fue bastante correcto. Los 3 supuestos que hizo realmente no afectaron mucho el resultado, por lo que se puede considerar que fueron bastante válidos dada las limitaciones de aquella época.
Ahora vayamos a Daftlogic.com y calculemos la distancia entre la ciudad de Alejandría y un punto en el mapa en donde exista la misma longitud de la de Alejandría (29.9192) y que esté ubicada exactamente en la línea del trópico que es la latitud 23° 26′ o 23.4377.
Si restamos las coordenadas de Alejandría y de la línea del trópico de cáncer nos da una distancia angular de 7.7604, lo que significa una 46.3894ava parte de una circunferencia y multiplicados por los 863.876 kms esto nos da 40, 074. Impresionante! Solo 66 kms de diferencia (un 0,16%) del calculo que actualmente se aproxima tiene la tierra.
Si ajustamos ahora el trópico de cáncer a la posición en la que se encontraba en el año -200 A.C, entonces encontraremos la verdadera medida de la sombra que se proyectó en la vara de Eratóstenes en Alejandría el 21 de junio al medio día hace 2,200 años: 7.4815 que es 7° 29′. Si trazamos la medida de 7.4815 en nuestro programa informático esto hace 48.1 partes de una circunferencia. 48 partes de una circunferencia multiplicados por los 863.876 km de distancia entre Alejandría y la línea del trópico hace 41,561 kms. Así que entre los errores de Eratóstenes tendríamos que agregar 0.2818 que es 0° 17′ grados de equivocación en la medición del ángulo de la sombra. Esto porque con un lápiz, o una punta fina, es imposible distinguir entre 7.0 y 7.2 grados, y muy difícil entre 7.0 y 7.5 grados. Era de esperarse que las divisiones de la circunferencia de Eratóstenes pudieran tener un margen de error de hasta 4 partes de una circunferencia. Se equivocaría en dos partes demás, lo cual no está mal considerando los instrumentos.
150 años después de Eratóstenes, el matemático también griego Posidonio, utilizó un método similar al de Eratóstenes (también descrito por Cleómedes en su obra), pero en vez de utilizar al sol como referencia, utilizó a una estrella llamada Canopus (la segunda estrella más brillante en el firmamento). Se dio cuenta de que en Rodhas esta estrella apenas se divisaba sobre el horizonte, pero estando en Alejandría esa estrella se encontraba más arriba en el cielo. Midió la longitud del arco que se trazaba entre las dos posiciones de la estrella, seguramente utilizando un astrolabio, y supongo que restando la medición del ángulo de la estrella en el cielo de Alejandría menos el ángulo en cielo de Rodas, para así encontrar la distancia angular entre Rodas y Alejandría. Pero la medición de Posidonio fue incorrecta. Le dio una distancia de 7. 5 grados o 7º 30′; cuando en realidad como vemos en el mapa, es de solo 4.97. Su error en la medición del ángulo debió haber radicado en que el astrolabio realmente no era muy preciso (aun menos los astrolabios primitivos), por eso fue reemplazado por el sextante 1,500 años después. La distancia entre Rodhas y Alejandría en realidad representa una 72ava parte de una circunferencia y no una 48ava parte.
Si hacemos el cálculo con los datos correctos nos da 42,014 kms. El cálculo de Posidonio resultó en 28,968 kilómetros (28 % de error con respecto a la circunferencia real de la tierra). Fue esta medición y no la de Eratóstenes la que utilizó Tolomeo en su famosa obra “Geographia”. Colón nunca leyó a Tolomeo, sino a otros autores de su epoca como Pierre de Ailly, quien basándose en el cálculo de Posidonio utilizado en Geographia, estimó la distancia entre las islas Canarias y Cipango (Japón). Pero Colón agregó otro error más al asunto, al suponer que Ailly hablaba de millas italianas cuando en realidad se refería a millas árabes (que son más largas). Colon creía que entre las islas Canarias y Cipango había unas 2,400 millas marinas, cuando en realidad había 10,700. Por suerte para el, se encontró un continente de por medio antes de llegar a Asia.
Este error en la medición de la circunferencia de la tierra ha sido seguramente el que más ha incidido en toda la historia de la humanidad. Si Colón hubiera sabido de la longitud de la circunferencia terrestre calculada por Eratóstenes, jamás hubiera realizado su viaje, pues ningún barco de aquella época podía almacenar agua y provisiones suficientes para permanecer tanto tiempo en altamar, y el descubrimiento de una ruta de ida y vuelta hacia América se hubiera retrasado quizá cientos de años.